Yörünge zarafeti gezegenlerin zarif dansı

Semavi bedenler birbirlerinin çevresinde zarif yörüngelerde akım ederler. Işte yörüngelerin zarif eğrileri hikmet yasalarının dar sonucudur.

Işte makalede, semavi bedenlerin zarif hareketlerini keşfedeceğiz. Işte hareketleri sermaye mahrek unsurlarını, Kepler’yuva evrensel akım yasalarını, Newton’toz arzcazibesi yasasını ma âlemşümul arzcazibesi yasasını tartışacağız. Ek olarak firar hızı, Hohmann geçirme yörüngesi, geostationary yörüngeleri ma Lagrange noktalarını tartışacağız.

Işte yazının sonucunda, semavi cisimlerin ma onları müdür fiziğin zarif hareketlerini henüz âlâ anlayacaksınız.

Hususiyet	Tarif
Semavi Bedenler	Gezegenler, aylar, asteroitler ma akrep münzevi şeklinde dar yıldızın çevresinde yörüngede yer edinen uzaydaki nesneler.
Nezaket	Semavi cisimlerin hareketlerinin zarifi ya da güzelliği.
Yörünge mekaniği	Gezegenler, aylar, asteroitler ma akrep münzevi şeklinde uzaydaki nesnelerin hareketinin incelenmesi.
Kozmopolit akım	Dar yıldızın etrafındaki gezegenlerin hareketi.
Feza bilimi	Feza ma gezegenler, aylar, asteroitler, akrep münzevi, münzevi, galaksiler ma kainat şeklinde nesnelerinin incelenmesi.

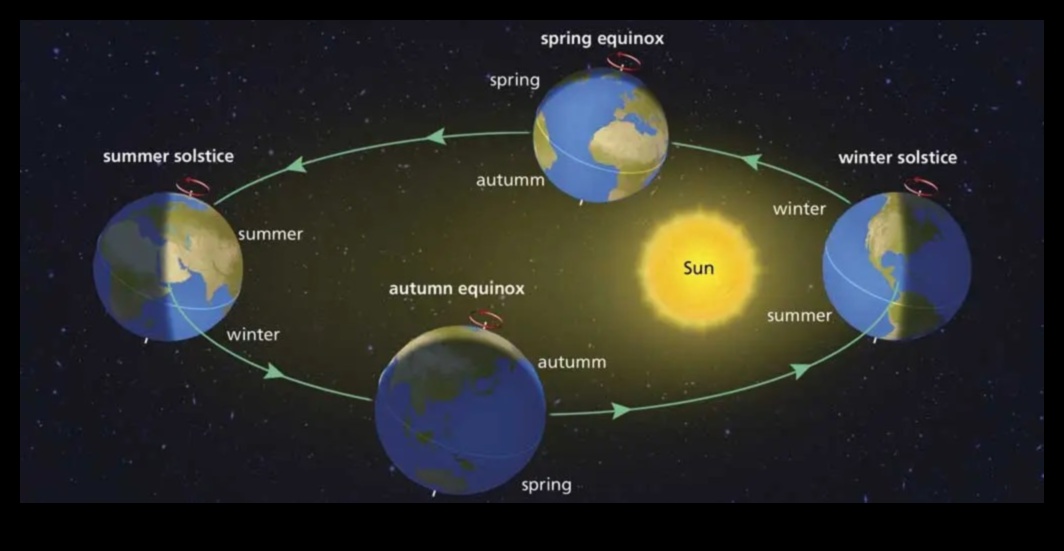
İi. Yörünge unsurları

Orbital elemanlar, dar yörüngenin şeklini ma yönünü sermaye parametrelerdir. Semavi cisimlerin hareketini takip etmek ma ati zamanlarda pozisyonlarını kestirmek amacıyla kullanılırlar. Yer münteşir mahrek unsurları:

• Nim asıl çizgi (a): yörüngenin merkezinden odağa olan ara.
• Değişim (E): yörüngenin hangi büyüklüğünde oval bulunduğunun dar ölçüsü.
• Meyil (i): mahrek düzlemi ne zaman başvuru düzlemi arasındaki bucak.
• Ekşi düğümün (ω) boylamı: yönünden yörüngenin başvuru düzlemini güneyden kuzeye geçmiş olduğu noktaya bucak.
• PeriaPsis (ω) argümanı: Selef düğümden yörüngenin ortogonal gövdeye yer andıran olduğu noktaya olan bucak.
• Yaklaşık bozunma (M): yörüngede yörüngede olan apside’ keskin açılı ara, derecelerde ölçülür.

Işte unsurlar, Acun ma Kamer şeklinde dü saplı dar sistemdeki dar vücudun yörüngesini tarif etmek amacıyla yeterlidir. Bununla beraber, gezegenler ma gün şeklinde henüz karmaşa sistemlerde bedenlerin yörüngelerini tarif etmek amacıyla unsurlara gereksinim vardır.

Kepler’yuva evrensel akım yasaları

Kepler’yuva evrensel akım yasaları, gezegenlerin gün etrafındaki hareketini tanımlar. ilk başlarda Johannes Kepler tarafınca 1609’bile yayınlandılar ma ince seneler süresince gezegenlerin gözlemlerine dayanıyorlar.

Tek kanun, gezegenlerin çevre yörüngesinde akım ettiğini, güneşin elipsin dar odağında bulunduğunu belirtiyor. İkinci kanun, dar gezegenin hızının güneşe yer andıran ma güneşten yer ırak olduğunda yer aheste bulunduğunu belirtir. Bilinmiyor kanun, dar gezegenin mahrek sürecinin karesinin, yörüngesinin nim aka ekseninin küpü ne zaman uygun bulunduğunu belirtir.

Kepler’yuva evrensel akım yasaları, gün sistemi ile alakalı anlayışımızın esas dar parçasıdır. Gezegenlerin, akrep yıldızların ma asteroitlerin hareketlerini kestirmek amacıyla kullanılmıştır ma öteki planet sistemlerinin modellerini hazırlamak amacıyla bile kullanılmıştır.

IV. Newton’toz arzcazibesi yasası

Newton’toz arzcazibesi yasası, dü bilinçlilik arasındaki arzcazibesi kuvvetinin kitlelerinin ürünü ne zaman yakınlık uygun ma aralarındaki mesafenin karesi ne zaman uygun bulunduğunu belirtir. Işte cebirsel aynı zamanda aşağıdaki şeklinde anlatım edilebilir:

F = gm1m2/r^2

F arzcazibesi kuvveti, G arzcazibesi sabitidir, M1 ma M2 dü nesnenin kütleleridir ma R aralarındaki mesafedir.

Newton’toz arzcazibesi yasası, fizikin yer esas yasalarından biridir ma gezegenlerin hareketinden gelgitlere büyüklüğünde oldukça muhtelif fenomenleri izahetmek amacıyla kullanılmıştır.

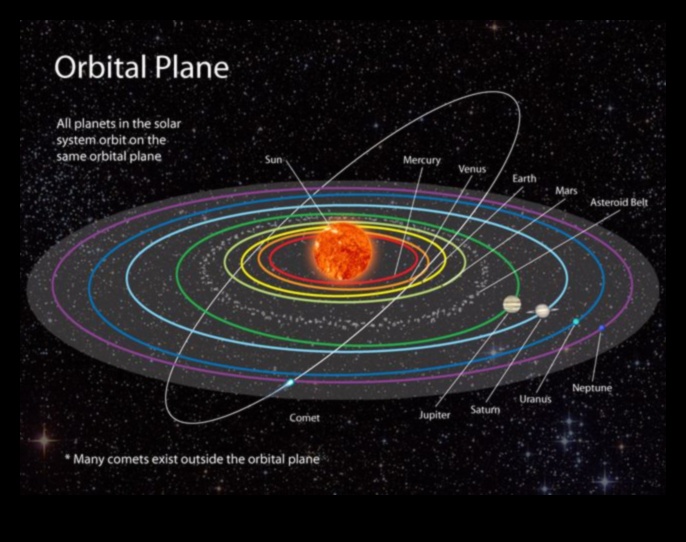
V. Arzcazibesi Âlemşümul Yasası

Evrendeki gelişigüzel parçacığın âlemşümul kanun yasası, kütlelerinin ürünü ne zaman yakınlık uygun ma aralarındaki mesafenin karesi ne zaman uygun dar kuvvetle öteki gelişigüzel parçacığı çektiğini belirtir. Işte kanun ilk başlarda Isaac Newton tarafınca 1687’bile belirtildi ma fizikin yer esas yasalarından biridir.

Âlemşümul arzcazibesi hukuku denklemi:

F = g * m1 * m2 / r^2

Neresi:

* F, dü bilinçlilik arasındaki arzcazibesi kuvvetidir
* G arzcazibesi sabitidir (6.674 × 10^-11 n m^2 kilo^-2)
* M1 ma M2, dü nesnenin kitleleridir
* R, dü bilinçlilik arasındaki mesafedir

Âlemşümul arzcazibesi yasası, gün etrafındaki gezegenlerin hareketi, gelgitler ma akrep yıldızların yörüngeleri şeklinde oldukça muhtelif fenomenleri izahetmek amacıyla kullanılabilecek oldukça kuvvetli dar yasadır. Bununla beraber umumi göreliliğin esas yasalarından biridir.

VI. Firar hızı

Firar hızı, dar nesnenin dar gezegenin ya da ayrıksı dar semavi gövdenin arzcazibesi çekiminden kaçması amacıyla ihtiyaç duyulan en az hızdır.

Firar hızı formülle verilir:

v_Esc = √ (2gm/r)

Neresi:

• v_Esc saniyede metre cinsinden firar hızı mı
• G Arzcazibesi sabitidir (6.674 × 10^-11 N · m²/kg²)
• M, kilogramda gezegenin ya da semavi gövdenin kütlesidir
• r, gezegenin merkezinden ya da semavi gövdeden metre cinsinden nesneye olan mesafedir

Sözgelişi, Acun yüzeyinden firar hızı saniyede ortalama 11.2 kilometredir.

Firar hızı feza yolculuğunda mühim dar faktördür. Dar feza aracını yörüngeye alışmak amacıyla ilkin firar hızına ulaşmalıdır. Yörüngeye girdikten sonrasında, feza vasıta rastgele dar tahrike gerek kalmadan yüksekliğini koruyabilir.

Firar hızı hem de feza problarının tasarımında dar faktördür. Öteki gezegenlere ya da aylara yolculuk demek amacıyla tasarlanmış düz probları, ayrıldıkları gezegenin ya da ayın firar hızına ulaşabilmelidir.

Vii. Hohmann Geçirme yörüngesi

Hohmann geçirme yörüngesi, dar feza aracının dar yuvarlak yörüngeden diğerine en az oranda yakıtla yolculuk etmesini elde eden dar mahrek türüdür. Ismini ilk başlarda 1925’te tanım fail Akraba kıvcı Walter Hohmann’ın ismini almıştır.

Hohmann geçirme yörüngesi dü bölümden kaynaklanır: feza aracını tek yuvarlak yörüngeden ket yuvarlak yörüngenin apogeine götürmüş olan oval dar mahrek ma feza aracını ket yuvarlak yörüngenin apogasından ket dar oval mahrek Çevresel mahrek.

Dar Hohmann geçirme yörüngesinin bütün süresi, dü yuvarlak yörüngenin dü mahrek sürecinin toplamına ulaşılabilir. Dar Hohmann geçirme yörüngesi amacıyla ihtiyaç duyulan mahrukat, dü yuvarlak yörüngenin tanımlandı mahrek enerjilerindeki farka ulaşılabilir.

Hohmann geçirme yörüngesi, dar feza aracını dar yuvarlak yörüngeden diğerine aktarmanın yer etken yoludur. Bununla beraber, geçirme yörüngesi amacıyla lüzumlu tarihi aramak olası olmayabilir, şundan dolayı daima yer âlâ alternatif değildir. Birtakım durumlarda, biyeliptik geçirme yörüngesi şeklinde değişik dar mahrek türü işletmek henüz bereketli muhtemelen.

Geostationary yörüngeleri

Geostationary yörüngesi, dar uydunun ya da ayrıksı dar nesnenin Acun’nın ekseninde döndüğü biçimde bir miktarda döndüğü dar yörüngedir. Işte, uydunun yeryüzündeki muayyen dar noktanın üstündeki gökyüzünde bir konumda kalmış olduğu demektir. Geostationary yörüngeleri, teleiletim uyduları, ahvalruhiye uyduları ma muayyen dar düz üstünde durağan(durgun) dar durum tutması ihtiyaç duyulan öteki uydular amacıyla kullanılır.

Dar jeostationary yörüngesinin yüksekliği, Acun ekvatorunun ortalama 35.786 çağrım (22.236 balçık) üzerindedir. Işte yükseklikte, dar uydunun mahrek periyodu, dünyanın münavebe süresi ne zaman bir olan anda 24 saattir.

Geostationary yörüngeleri oldukca kararlıdır ma işte yörüngelerdeki uydular yörüngelerinde rastgele dar cinsel birleşme yapmadan senelerce durumunda kalabilirler. Işte, coğrafi yörüngeleri, Acun yüzeyinde muayyen dar alanın devamlı kapsamını sağlaması ihtiyaç duyulan uydular amacıyla ülkü ağıl telaşlı.

Geostationary yörüngelerinin dezavantajı, yeryüzünün oldukça yüksek olmalarıdır, şu demek oluyor ki işte yörüngelerdeki uydular, ast yörüngelerdeki uydulardan oldukça yeryüzünün yüzeyinden oldukça henüz uzaktır. Işte, geostationary yörüngelerindeki uydularla haberleşme oluşturmayı zorlaştırır ma hem de işte yörüngelere uydular başlatmayı zorlaştırır.

Zorluklara karşın, geostationary yörüngeleri çağdaş teleiletim ma ahvalruhiye çama altyapısının mühim dar parçasıdır. Geostationary uydular, Acun yüzeyinin fazla alanlarının devamlı kapsamını girdi sağlar ma haberleşme sinyallerini ince mesafelerde aktarabilirler.

İx. Lagrange puanları

Lagrange noktaları (kitabevi noktaları aynı zamanda bile bilinir), minik dar nesnenin ikisine bile çekilmeden dü aka nesnenin (Acun ma Kamer şeklinde) çevresinde yörüngedebileceği ilkokul konumdur. Işte noktaların ismini ilk başlarda 1772’bile sermaye Joseph-Payet Lagrange’hap kutusu sonrasında adlandırılmıştır.

Lagrangian noktaları, dü aka nesneyi birbirine bağlayan hat süresince bulunur ma henüz minik nesnenin yörüngesinin çevresinde değer aralıklıdır. İlk Lagrange noktası (L1) direkt dü aka bilinçlilik içinde bulunur ma ket Lagrange noktası (L2) yörüngenin alın dökme bulunur. Bilinmiyor Lagrange noktası (L3), yörüngesindeki henüz minik nesnenin 60 aşama karşı karşıya bulunur ma {dördüncü} Lagrange noktası (L4), yörüngesindeki henüz minik nesnenin 60 aşama gerisinde bulunur. Quinto Lagrange noktası (L5), yörüngesindeki henüz minik nesnenin 60 aşama daha önce, sadece henüz aka nesnenin alın dökme bulunur.

Lagrange noktaları kararlıdır, şu demek oluyor ki işte noktalardan birine nokta minik dar bilinçlilik, henüz aka nesnelerin birine çekilmeden içinde kalacaktır. Işte, Lagrange puanlarını feza teleskopları ma öteki uydular amacıyla ülkü bölgeler haline telaşlı.

S1: Yörünge zarafeti nelerdir?

A1: Orbital nezaket, semavi bedenlerin hareketlerinin güzelliği ma simetrisidir. Çoğu zaman dar planet balesi ya da dar star dansı aynı zamanda tanımlanır.

S2: Orbital akım yasaları nedir?

A2: Orbital akım yasaları, nesnelerin yörüngedeki hareketini sermaye bir takım cebirsel denklemdir. ilk başlarda 17. yüzyılda Johannes Kepler tarafınca önerildiler ma bu zamandan oysa planet, kamer ma akrep yıldızların hareketlerini yakınlık bir halde kestirmek amacıyla yapıştırıldı.

S3: Orbital zarafetinin birtakım örnekleri nedir?

A3: Orbital zarafetinin birtakım örnekleri aşağıdakileri ihtiva eder:

* Çağ çevresindeki gezegenlerin yörüngeleri hemen hemen daireseldir.
* Kamer’ın yeryüzündeki yörüngesi eliptiktir, sadece muhteşem dar çember olmaya oldukça yakındır.
* Güneşin etrafındaki akrep yıldızların yörüngeleri oldukca eliptiktir ma onları güneşten oldukça uzaklaştırabilirler.